好久没有写博客了，今天要开始重新捡起来了。

距离

概念

设$X=(x_1,x_2,\dots,x_n),Y=(y_1,y_2,\dots,y_n)$

L1距离 (Manhattan distance 中文：曼哈顿距离)

$d_1(X,Y)=\sum^n_{i=1}|x_i-y_i|_1$

L2距离 (Euclidean distance 中文：欧式距离)

$d_2(X,Y)=\sqrt{\sum^n_{i=1}(X_i-Y_i)^2}$

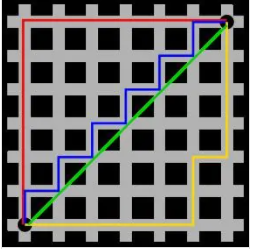
图中红线代表曼哈顿距离，绿线代表欧氏距离也就是直线距离而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即$d(i,j)=|x_i-x_j|+|y_i-y_j|$。对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。曼哈顿距离不是距离不变量，当坐标轴变动时，点间的距离就会不同。曼哈顿距离示意图在早期的计算机图形学中，屏幕是由像素构成，是整数，点的坐标也一般是整数，原因是浮点运算很昂贵，很慢而且有误差，如果直接使用AB的欧氏距离（欧几里德距离：在二维和三维空间中的欧氏距离的就是两点之间的距离），则必须要进行浮点运算，如果使用AC和CB，则只要计算加减法即可，这就大大提高了运算速度，而且不管累计运算多少次，都不会有误差。

图片和描述摘自曼哈顿距离_百度百科 (baidu.com)

图像

以二维空间为例：对于L1，他计算的是第一维差的绝对值加上第二维差的绝对值，可以想象成直角三角形的两条直角边的长度和。对于L2，他计算的是第一维差的平方加上第二维差的平方再求和，然和开根。由勾股，可以想象成直角三角形的斜边长。当距离一定时，若以$X$为原点，则$Y$所有可能的点即为上述图像。

$以二维空间为例 \\ d_1=|x_1-x_2|+|y_1-y_2|, d_2=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\\ 当 X 为原点时，即X=(x_1,y_1)=(0,0) \\ d_1 = |x_2|+|y_2|, \\ d_2 = \sqrt{x_2^2+y_2^2}, d^2_2= x_2^2+y_2^2 \\$

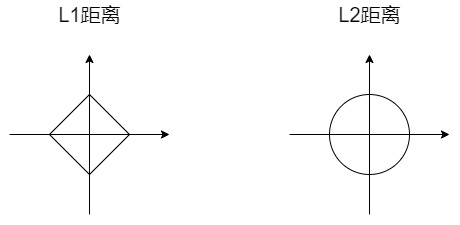
注意区分：

L2范数

设X是n维特征$X=(x_1,x_2,\dots,x_n)$

$||x||_2=\sqrt{\sum^n_{i=1}x^2_i}$

闵可夫斯基距离

p是一个变量，当p=2的时候就得到欧式距离

$D(X,Y)=(\sum^n_{i=1}|x_i-y_i|^p)^{\frac{1}{p}}$

损失函数

L1和L2都可以做损失函数使用。

L2损失函数

L2范数损失函数，也被称为最小平方误差（LSE）。它是把目标值 $y_i$ 与估计值 $f(x_i)$ 的差值的平方和最小化。一般回归问题会使用此损失，离群点对次损失影响较大。

$L=\sum^n_{i=1}(y_i-f(x_i))^2$

L1损失函数

也被称为最小绝对值偏差（LAD），绝对值损失函数（LAE）。总的说来，它是把目标值 $y_i$ 与估计值 $f(x_i)$ 的绝对差值的总和最小化。

$L=\sum^n_{i=1}|y_i-f(x_i)|$

二者对比

L1损失函数相比于L2损失函数的鲁棒性更好。

因为L2范数将误差平方化（如果误差大于1，则误差会放大很多），模型的误差会比L1范数大的多，因此模型会对这种类型的样本更加敏感，这就需要调整模型来最小化误差。但是很大可能这种类型的样本是一个异常值，模型就需要调整以适应这种异常值，那么就导致训练模型的方向偏离目标了。

损失函数参考L1和L2 详解(范数、损失函数、正则化) - 知乎 (zhihu.com)

写的不错的博客【损失函数】损失函数专题 - 梁君牧 - 博客园 (cnblogs.com)